最短路径算法

文章目录

1. 引入
2. 最短路径的解决算法
3. Dijkstra算法
1. 3.0.0.1. 定义概览
2. 3.0.0.2. 算法描述
3.0.1. 代码

4. 例题

4.1. 路径
1. 4.1.0.1. 代码

引入

假设一个开车的人希望找出从新疆到北京的可能的最短路线。他有一张中国公路地图，该公路图上标出了每一对相邻的公路交叉之间的距离，他应该如何找出这一最短路线呢？

一种可能的方法就是枚举出所有从新疆到北京之间的路线，依然存在着数以百万计的行车路线，而其中绝大多数是不值得考虑的。

现实中很多抽象的例子都可以转化成类似这样的问题，这类问题统一称为求最短路径的问题。

最短路径的解决算法

Floyd
求多源、无负权边的最短路。用矩阵记录图。时效性较差，时间复杂度O(V^3)。
Dijkstra
求单源、无负权的最短路。时效性较好，时间复杂度O(V^2)。
Bellman-Ford
求单源最短路，可以判断有无负权回路。通过不断构建以源点为根的最短路径树，不断扩展。
SPFA
可以用于存在负数边权的图，算法时间效率是不稳定的，即它对于不同的图所需要的时间有很大的差别。SPFA算法是在Bellman-Ford算法的基础上进行优化而来。

Dijkstra算法

定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

算法描述

算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

算法步骤：

初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。
以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值为顶点k的距离加上<k,u>边上的权。
重复步骤 2 和 3 直到所有顶点都包含在 S 中。

Tip:
通常在编码过程中，以一个二维数组map[][]来表示整张图，以一个一维数组dist[]来表示源点到各个顶点的当前最短路径，以一个一维数组set[]来标识当前顶点是否已经被并入到集合S中，即当前顶点的最短路径已经求出。

执行动画:

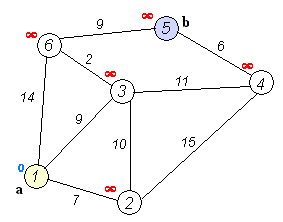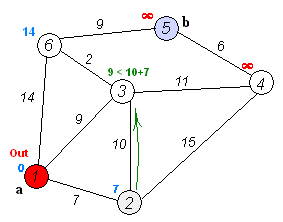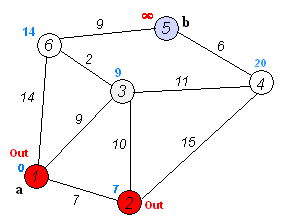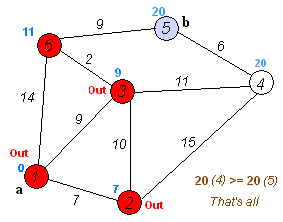
dijkstra_img

代码

由上述讲解可以写出如下Dijkstra算法代码

// 图的存储在 MGraph  g.n为顶点数量 g.edges[][]为边的权值
// v为源点
// dist[] 保存源点到各个顶点的当前最短路径
void Dijkstra(MGraph g, int v, int dist[]) {
    int set[maxSize];
    int min,i,j,u;
    // 初始化
    for(i = 0;i<g.n;i++) {
        dist[i] = g.edges[v][i];
        set[i] = 0;
    }
    set[v] = 1;
    
    for(i = 0;i < g.n; i++ ) {
        min = INF;
        // 这个循环每次从剩余顶点中选出一个顶点，通往这个顶点的路径在通往所有剩余顶点的路径中是长度最短的
        for (j = 0;j< g.n;j++) {
            if(set[h] == 0 && dist[j] < min) {
                u = j;
                min = dist[j];
            }
        }
        set[u] = 1;
        // 以刚并入的顶点作为中间点，对所有通往剩余顶点的路径进行检测
        for (j = 0;j < g.n;j++) {
            if (set[j]==0&&dist[u]+g.edges[u][j]<dist[j]) {
                dist[j] = dist[u]+g.edges[u][j];
            }
        }
    }
    
}

例题

例如经典的题目HDU1874。

问题描述：

某省自从实行了很多年的畅通工程计划后，终于修建了很多路。不过路多了也不好，每次要从一个城镇到另一个城镇时，都有许多种道路方案可以选择，而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。
现在，已知起点和终点，请你计算出要从起点到终点，最短需要行走多少距离。

Input:

本题目包含多组数据，请处理到文件结束。
每组数据第一行包含两个正整数N和M(0<N<200,0<M<1000)，分别代表现有城镇的数目和已修建的道路的数目。城镇分别以0～N-1编号。
接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B<N,A!=B,0<X<10000),表示城镇A和城镇B之间有一条长度为X的双向道路。
再接下一行有两个整数S,T(0<=S,T<N)，分别代表起点和终点。

Output:

对于每组数据，请在一行里输出最短需要行走的距离。如果不存在从S到T的路线，就输出-1.

解析：

这是典型的求解最短路径的问题，可以把城镇转换成图中的点，道路转换成图中的有权边，然后根据构造出的这张图，求解源点到各个点的最短路径即可。

代码：

#include "stdio.h"
#define MAX_INT 10000
//
int set[202];
int map[202][202];
int dis[202];


void Dijkstra(int start , int n) {
    
    // 初始化
    for (int i = 0; i<n; i ++) {
        dis[i] = map[start][i];
        set[i] = 0;
    }
    set[start] = 1;
    
    for (int j = 0 ; j < n; j ++) {
        
        // 找当前最短路径
        int temp = MAX_INT;
        int u = start;
        for (int i = 0; i < n; i ++) {
            if (set[i] == 0 && dis[i] < temp) {
                temp = dis[i];
                u = i;
            }
        }
        set[u] = 1;
        
        // 以u为中间点更新最短路径
        for (int i = 0 ; i < n; i ++) {
            if (set[i] == 0 && dis[u] + map[u][i] < dis[i]) {
                dis[i] = dis[u] + map[u][i];
            }
        }
    }
    
}

int main(int argc, const char * argv[]) {
    int n,m;
    int a,b,c;
    while (scanf("%d %d",&n,&m) != EOF) {
        // 图的初始化
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < n; j ++) {
                if (i == j) {
                    map[i][j] = 0;
                } else {
                    map[i][j] = MAX_INT;
                }
            }
        }
        while (m--) {
            scanf("%d%d%d",&a,&b,&c);
            if (c < map[a][b]) {
                map[a][b] = map[b][a] = c;
            }
        }
        int start , end;
        scanf("%d%d",&start,&end);
        Dijkstra(start, n);
        if (dis[end] == MAX_INT) {
            printf("-1\n");
        } else {
            printf("%d\n",dis[end]);
        }
    }
    return 0;
}

几个变形题目，可以当做练习：

练习题

password:123

路径

经过以上步骤，我们已经求出了源点到各个顶点的最短路径的值，如果此时需要知道该最短路径所上所经过的点，该如何解决呢？

此时我们可以用一个一维数组path[]来保存最短路径上所经过的订单。
比如：path[Vi]中保存从源点到Vi的最短路径上Vi的前一个顶点，假设最短路径上的顶点序列为V0,V1,V2,V3,...,Vi-1,Vi 则path[Vi]=Vi-1。

path[]测初态为：假设V0为源点，如果V0到Vi有边，则path[Vi]=V0,否则path[Vi]=-1。
在上面的步骤中，每一次更新最短路径的值的时候，同时更新path[]的值，直到所有的顶点的最短路径更新完毕，path[]中也就保存了每个最短路径所经历的顶点，这是一个树形结构。

代码

在上面的代码上做一些修改,增加了path[]数组：

// 图的存储在 MGraph  g.n为顶点数量 g.edges[][]为边的权值
// v为源点
// dist[] 保存源点到各个顶点的当前最短路径
// path[] 保存从源点到`Vi`的最短路径上`Vi`的前一个顶点
void Dijkstra(MGraph g, int v, int dist[], int path[]) {
    int set[maxSize];
    int min,i,j,u;
    // 初始化
    for(i = 0;i<g.n;i++) {
        dist[i] = g.edges[v][i];
        set[i] = 0;
        // path[] 初始化
        if (g.edges[v][i] < INF) {
        	path[i] = v;
        } else {
        	path[i] = -1;
        }
    }
    set[v] = 1;
    path[v] = -1;
    
    for(i = 0;i < g.n; i++ ) {
        min = INF;
        // 这个循环每次从剩余顶点中选出一个顶点，通往这个顶点的路径在通往所有剩余顶点的路径中是长度最短的
        for (j = 0;j< g.n;j++) {
            if(set[h] == 0 && dist[j] < min) {
                u = j;
                min = dist[j];
            }
        }
        set[u] = 1;
        // 以刚并入的顶点作为中间点，对所有通往剩余顶点的路径进行检测
        for (j = 0;j < g.n;j++) {
            if (set[j]==0&&dist[u]+g.edges[u][j]<dist[j]) {
                dist[j] = dist[u]+g.edges[u][j];
                path[j] = u;
            }
        }
    }
    
}

骚客

菩提本无树，明镜亦非台。本来无一物，何处惹尘埃！

最短路径算法

引入

最短路径的解决算法

Dijkstra算法

定义概览

算法描述

代码

例题

路径

代码